En el ámbito de la investigación científica, la calidad de la muestra es fundamental para la generalización, es decir, para garantizar que los resultados obtenidos son válidos y aplicables al conjunto de la población. Además, hay que indicar que, afortunadamente, la capacidad de generalización de la investigación es bastante robusta respecto a las variaciones en la calidad de la muestra. O, dicho de otra forma, la investigación felizmente puede tolerar muestras imperfectas (Blair y Zinkhan, 2006) sin un riesgo severo de descalabro para los resultados. Pero, ¿son todas las muestras imperfectas igual de “imperfectas”?
Consideremos, por ejemplo, que queremos realizar una investigación sobre el proceso de adopción por parte de los consumidores de un nuevo producto. Una opción al alcance de muchos investigadores es utilizar una muestra de estudiantes de la universidad en la que imparten docencia. Si el incentivo es atractivo para el estudiante, es posible incluso alcanzar una tasa de respuesta que se aproxime al 100%. ¿Es esta muestra mejor que una que suponga, por ejemplo, una tasa de respuesta del 15%, sobre un conjunto de consumidores en el que hay algún esfuerzo de representación (en edad, ingresos, estudios…) de la población a la que se dirige tal producto?
No es erróneo pensar que una muestra grande es mejor que una pequeña, pero siempre y cuando el incremento del tamaño no se haga a costa de la representatividad, ya que una muestra grande per se no garantiza resultados generalizables. No debemos confundir tamaño con representatividad. Aunque ambos conceptos están relacionados, no son sinónimos y su confusión puede llevar a decisiones equivocadas.
El tamaño de la muestra se refiere al número de observaciones o individuos incluidos en el estudio. Es un aspecto cuantitativo que, en teoría, cuanto mayor sea, más precisa será la estimación de los parámetros poblacionales. Un tamaño de muestra grande puede reducir el error estándar y aumentar la precisión de las estimaciones. Sin embargo, no garantiza por sí mismo que la muestra sea representativa de la población. La representatividad, por otro lado, es una característica cualitativa que indica en qué medida la muestra refleja las características de la población de la que se ha extraído. Una muestra representativa debe ser un microcosmos de la población, de su diversidad, por lo que debe responder a las proporciones de las diferentes subpoblaciones presentes en ella.
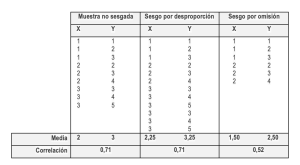
En la tabla siguiente hemos recogido el ejemplo de Blair y Zinkhan (2006) en el que se compara una muestra no sesgada con dos muestras sesgadas: una con un sesgo por desproporción de un grupo de población y otra con un sesgo por omisión. En el ejemplo se observa que, aunque una muestra sesgada puede afectar a las estimaciones univariadas (la media de las variables X e Y cambia, tanto para la muestra con sesgo por desproporción, como para la muestra con sesgo por omisión, respecto a la muestra sin sesgo), los sesgos en las estimaciones de relaciones entre variables (basadas en la correlación), en los que se centra una buena parte de la investigación académica, tienden a ser menores en los sesgos por desproporción que por omisión.
Que de la población a la que queremos estudiar logremos una baja tasa de respuesta, no es deseable. Pero la falta de respuesta es solo una de las fuentes de posible sesgo, y no es la peor. Para una generalización fiable de los resultados es más determinante la diversidad que el tamaño de la muestra. Una muestra grande y no representativa puede dar una falsa y peligrosa sensación de seguridad sobre la validez de los resultados obtenidos.
Ana Isabel Rodríguez Escudero


Deja tu comentario